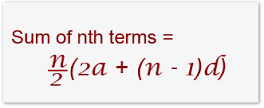
Introduction
Arithmetic Progression, Generally called as AP is a set of numbers which are having constant difference between their consecutive numbers. In other way we can say – A list of numbers having specific relation between the consecutive terms is generally called a sequence.
Ex. The sequence 5, 7, 9, 11, 13, 15 … is an arithmetic progression with common difference of 2.
Formulas at a Glance
If
then
- 1.
- 2.
- 3.
![S_n=\frac{n}{2}[ 2a_1 + (n-1)d].](https://wikimedia.org/api/rest_v1/media/math/render/svg/d534b9366b68311f06e07cc3d22b25f588ee318b)
- 4.
- 5. n ¯ =
- 6.
Important Facts
There are many important facts about AP, please find below –
- The general form of Arithmetic progression is a, a+d, a+2d, a+3d,……….,a+(n-1)d
Where a = First Term in the list, d = Common Difference
- Common Difference (d) can obtain by subtracting number from the list with it’s immediate previous number. like Series a1, a2, a3, a4,…………………………. have common difference as (a2-a1).
d= (a3-a2)
Ex. Series 1,3,5,7,9…. is having common difference as 2.
Tutorial Video(s)
Part1
Exercise 1
Video Explain above Exercise
Exercise 2
Video Explain above Exercise
Sum Of AP
This section contain information about summation of Arithmetic Progression, Please follow below videos –
Very good tutorial and easy to understand… Keep it up… Good luck
What is the least number of terms required for the sum less than (-500) to be formed in this arithmetic progression when its first term is 1 and Common difference is (-2)?
What is the least number of terms required for the sum less than (-500) to be formed in this (3-2 k) rithmetic progression when its first term is 1 and Common difference is (-2)?
least term will be 23 term…