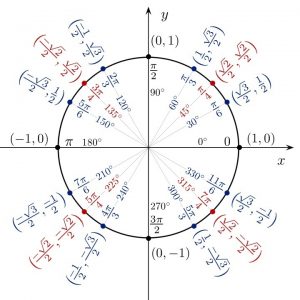
Introduction
This post contains important formulas related Trigonometric Identities. These formulas will help to solve many trigonometric problems.
0 < θ < Π/2 OR 0′ < θ < 90′
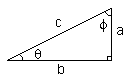
θ = theta
Basic Trigonometric Formula
sin(θ) = a / c
csc(θ ) = 1 / sin(θ ) = c / a
cos(θ) = b / c
sec(θ ) = 1 / cos(θ) = c / b
tan(θ) = sin(θ) /cosθ) = a / b
cot(θ) = 1/ tan(θ) = b / a
Even/Odd Formulas
sin(-θ) = -sin(θ)
csc(-θ) = -csc(θ)
cos(-θ) = cos(θ)
sec(-θ) = sec(θ)
tan(-θ) = -tan(θ)
cot(-θ) = -cot(θ)
Pythagorean Identities
sin^2(θ) + cos^2(θ) = 1
tan^2(θ) + 1 = sec^2(θ)
cot^2(θ) + 1 = csc^2(θ)
Sum and Difference Formulas
sin(θ1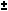 
θ2) = sin θ1 cosθ2 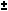cos θ1 sin θ2
cos(θ1 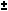θ2) = cosθ1 cosθ2 
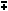sin θ1 sinθ2
tan(θ1 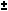θ2) = (tan θ1 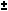tanθ2) / (1 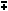tanθ1 tanθ2)
Double Angle Formulas
sin(2θ) = 2 sinθ cosθ
cos(2θ) = cos^2(θ) – sin^2(θ) = 2 cos^2(θ) – 1 = 1 – 2 sin^2(θ)
tan(2θ) = 2 tan(θ) / (1 – tan^2(θ))
sin^2(θ) = 1/2 – 1/2 cos(2θ)
cos^2(θ) = 1/2 + 1/2 cos(2θ)
Sum to Product Formulas
sinθ1 + sinθ2 = 2 sin( (θ1 + θ2)/2 ) cos( (θ1 1 θ2)/2 )
sinθ1 – sinθ2 = 2 sin( (θ1 – θ2)/2 ) cos( (θ1 + θ2)/2 )
cosθ1 + cosθ2 = 2 cos( (θ1 + θ2)/2 ) cos(θ1 – θ2)/2 )
cosθ1 – cosθ2 = -2 sin( (θ1 – θ2)/2 ) sin(θ1 + θ2)/2 )
Sum and Difference Formulas
sin(θ1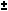θ2) = sinθ1 cosθ2 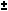cosθ1 sinθ2
cos(θ1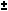θ2) = cosθ1 cosθ2 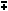sinθ1 sinθ2
tan(θ1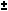θ2) = (tanθ1 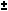tanθ2)/(1 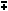tanθ1tanθ2)
Product to Sum Formulas
sinθ1sinθ2 = 1/2[cos(θ1–θ2) – cos(θ1+θ2)]
cosθ1cosθ2 = 1/2[cos(θ1–θ2) + cos(θ1+θ2)]
sinθ1cosθ2 = 1/2[sin(θ1+θ2) + sin(θ1–θ2)]
cosθ1sinθ1 = 1/2[sin(θ1+θ2) – sin(θ1–θ2)]
Given Triangle abc, with angles A,B,C; a is opposite to A, b opposite B, c opposite C:
a/sin(A) = b/sin(B) = c/sin(C) (Law of Sines)
|
(Law of Cosines) |
(a – b)/(a + b) = tan [(A-B)/2] / tan [(A+B)/2] (Law of Tangents)
Range
The range is all possible values to get
out of the function.
-1 <= sinθ <=1 cscθ >= 1 and cscθ<=-1
-1 <= cosθ <=1 -1<= secθ and secθ<=1
-∞ < tanθ <∞ -∞< cotθ < ∞
Tangent and Cotangent Identities
tanθ = sinθ/cosθ
cotθ = cosθ/sinθ
Reciprocal Identities
sinθ = 1/cscθ
cscθ = 1/sinθ
cosθ = 1/secθ
secθ = 1/cosθ
tanθ = 1/cotθ
cotθ = 1/tanθ
Periodic Formulas
If n is an integer.
sin(θ + 2πn) = sinθ
csc(θ + 2πn) = cscθ
cos(θ + 2πn) = cosθ
sec(θ + 2πn) = secθ
tan(θ + 2πn) = tanθ
cot(θ + 2πn) = cotθ
Cofunction Formulas
π/2 – θ :
sin(π/2 – θ) = cosθ
cos(π/2 – θ) = sinθ
tan((π/2 – θ) = cotθ
cot(π/2 – θ) = tanθ
sec(π/2 – θ) = cosecθ
cosec(π/2 – θ) = secθ
π/2 + θ:
sin(π/2 + θ) = cosθ
cos(π/2 + θ) = -sinθ
tan((π/2 + θ) = -cotθ
cot(π/2 + θ) = -tanθ
sec(π/2 + θ) = -cosecθ
cosec(π/2 + θ) = secθ
3π/2 – θ:
sin(3π/2 – θ) = -cosθ
cos(3π/2 – θ) = sinθ
tan((3π/2 – θ) = -cotθ
cot(3π/2 – θ) = -tanθ
sec(3π/2 – θ) = cosecθ
cosec(3π/2 – θ) = –secθ
3π/2 + θ:
sin(3π/2 + θ) = –cosθ
cos(3π/2 + θ) = -sinθ
tan((3π/2 + θ) = cotθ
cot(3π/2 + θ) = tanθ
sec(3π/2 + θ) = -cosecθ
cosec(3π/2 + θ) = –secθ
π – θ:
sin(π – θ) = sinθ
cos(π – θ) = -cosθ
tan(π – θ) = -tanθ
cot(π – θ) = -cotθ
sec(π – θ) = -secθ
cosec(π – θ) = cosecθ
π + θ:
sin(π + θ) = –sinθ
cos(π + θ) = cosθ
tan(π + θ) = -tanθ
cot(π + θ) = -cotθ
sec(π + θ) = secθ
cosec(π + θ) = –cosecθ
Degrees to Radians Formulas
If x is an angle in degrees and t is an
angle in radians then
Π/180 = t/x ⇒ t = Πx/180 ⇒ x = 180t/Π
Trig Table of Common Angles
| angle (degrees) | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 = 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| angle (radians) | 0 | PI/6 | PI/4 | PI/3 | PI/2 | 2/3PI | 3/4PI | 5/6PI | PI | 7/6PI | 5/4PI | 4/3PI | 3/2PI | 5/3PI | 7/4PI | 11/6PI | 2PI = 0 |
| sin(a) |  (0/4) |
(1/4) |
(2/4) |
(3/4) |
(4/4) |
(3/4) |
(2/4) |
(1/4) |
(0/4) |
–(1/4) |
–(2/4) |
–(3/4) |
–(4/4) |
–(3/4) |
–(2/4) |
–(1/4) |
(0/4) |
| COs(a) | (4/4) |
(3/4) |
(2/4) |
(1/4) |
(0/4) |
–(1/4) |
–(2/4) |
–(3/4) |
–(4/4) |
–(3/4) |
–(2/4) |
–(1/4) |
(0/4) |
(1/4) |
(2/4) |
(3/4) |
(4/4) |
| tan(a) | (0/4) |
(1/3) |
(2/2) |
(3/1) |
(4/0) |
–(3/1) |
–(2/2) |
–(1/3) |
–(0/4) |
(1/3) |
(2/2) |
(3/1) |
(4/0) |
–(3/1) |
–(2/2) |
–(1/3) |
(0/4) |
PI = Π
One thought on “Trigonometric Identities Formula”